Types of Skewness

The types of skewness is studied in relation to the shape of the frequency curve of the frequency distribution of data.

What is Skewness and types of skewness in Statistics?

Before understanding the types of skewness, let’s understand the meaning of skewness and frequency distribution first.

As we know every frequency distribution needs to be symmetrical or symmetrically distributed, but there are a lot of factors that affect the data, classification, and interpretation of variables.

These factors take the values far from the symmetry. Hence, this is known as skewness of frequency distribution.

The symmetrical frequency distribution is represented in the bell-shaped graph below:

 

Meaning of Skewness

The lack of symmetry of a frequency distribution is called skewness. In other words, a frequency distribution whose frequency curve is not bell-shaped is said to be skewed.

Meaning of Frequency Distribution

While doing the classification of data, values of variable under study are considered. This is known as classification of data or Frequency distribution.

Types of Skewness

The skewness of frequency distribution can be of two types:

(1) Positive Skewness 

 

(2) Negative skewness

It should be remembered that zero skewness is not considered one of the types of skewness, because a frequency distribution with zero skewness is not skewed but it is symmetric.

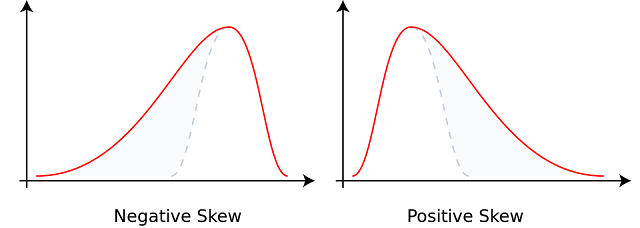
1. Positive Skewness or Positively Skewed Distribution

The frequency curve of the positively skewed frequency distribution is as shown in the above diagram-

A frequency distribution in which the values of the mean, median, and mode are in descending order i.e. x̄ > M > Z, is said to be a positively skewed frequency distribution.

In frequency distribution with positive skewness, the distance between the third quartile and the median is greater than the distance between the median and the first quartile. i.e. Q₃ - M > M - Q₁

In such a frequency distribution, the right tail of its frequency curve is more elongated than the left tail.

2. Negative Skewness or Negatively Skewed Distribution

The frequency curve of the negatively skewed frequency distribution is as shown in the above diagram-

A frequency distribution in which the values of the mean, median, and mode are in ascending order i.e. x̄ < M < Z, is said to be a negatively skewed frequency distribution.

In frequency distribution with Negative skewness, the distance between the third quartile and the median is less than the distance between the median and the first quartile.i.e. Q₃ - M < M - Q₁

In such a frequency distribution, the left tail of its frequency curve is more elongated than the right tail.

After learning the types of skewness lets also understand the “Tests of Skewness”

We know that the lack of symmetry of a frequency distribution is called skewness. To decide whether a given frequency distribution is skewed or not the following tests can be used.

(1) A frequency distribution in which the values of the mean, median, and mode are not equal.

(2) If both the quartiles i.e. the first and third quartiles are equidistant from the median, then such a frequency distribution is said to be skewed.

(3) If the frequency curve of the frequency distribution is not bell-shaped then it is said to be skewed.

(4) Frequency distribution in which the frequencies of the classes which are located equidistant from the middle class are not equal is said to be skewed frequency distribution.

(5) If the right tail or the left tail of the frequency curve is more elongated then the frequency distribution is said to be skewed frequency distribution.

Skewness and co-efficient of skewness

(Absolute and Relative Measures of Skewness)

Skewness: Skewness is a lack of symmetry in a frequency distribution. Skewness is an absolute measure and it is denoted by 'sk'. 

Skewness is not independent of units of measurement, i.e. it is expressed in the units of the given data.

Co-efficient of Skewness: The relative measure of skewness of frequency distribution is called co-efficient of skewness and it is denoted by 'j'. 

The coefficient of skewness is independent of units of measurement, i.e. it is a simple number free from the units of the given data.

Types of skewness with Examples. 

Symmetric:

If Q₃ + Q₁=60 and M=30, then state the type of skewness.

Ans: Sk = Q₃ + Q₁ - 2M

= 60 - 2(30) = 60 - 60 = 0

There is zero skewness. i.e. Frequency distribution is symmetric. 

Negative Skewness:

For a frequency distribution 3Q₃ = 8Q₁ = 4M =120. Then find its skewness.

Ans: 3Q₃ = 120 so, Q₃ = 40

         8Q₁ = 120 so, Q₁ = 15 

       4M = 120 so, M = 30

Now, Skewness = Q₃+ Q₁ - 2M 

so, 40 + 15 - 2(30) = -5

so, Sk = -5 

Positive Skewness:

The median and the mean of a data set are 52 and 55 respectively. State the type of skewness.

Ans: Here, median (M) = 52 and mean (X̅) = 55

Now, Sk = 3(X̅- M) = 3 (55 - 52) = 3 (3) = 9

Hence, mean > median, therefore there is positive skewness in the data.

Methods of determining Skewness and the coefficient of Skewness.

If a frequency curve of a given frequency distribution is drawn, then it can be known whether the skewness is positive or negative. But the numerical measure of skewness can not be known. Also, it is necessary to find numerical measures of skewness for comparison of two or more frequency distributions. For determining skewness and the coefficient of skewness following two methods are used.

(I) Karl Pearson’s Method

(II) Bowley’s Method

(1) Karl Pearson’s Method:

Base: In a skewed frequency distribution, the values of the mean, median, and mode are not equal i.e.  X̅ not equal to M not equal to Z. Also, the median always lies between the mean and mode. Karl Pearson’s method is based on this test of skewness.

Formulae: Skewness is the difference between the mean and mode.

i.e. skewness (sk) = X̅ - Z

The coefficient of skewness is obtained by dividing the above difference by standard deviation (S).

i.e. coefficient of Skewness (j) = X̅ - Z / S

When the frequency distribution is not unimodal or otherwise the mode is ill-defined, then mode can be obtained by the formula Z = -3M – 2X̅

Hence, when a mode is ill-defined then the following formulae are used.

Skewness (sk) = 3 (X̅ - M)

Coefficient of Skewness (j) = 3 (X̅ - M) / S

Note:

(i) The value of the coefficient of skewness given by formula 3 ( X̅ - M) / S always lies between between  -1.73 and +1.73 for any uni-modal skewed frequency distribution. 

This has been proved by statistician N.L. Johnson in the year 1951. But generally, in practice, the value of j based on a sample lies between -1 and +1 for skewed frequency distribution.

(ii) The value of the coefficient of skewness given by formula j = 3 ( X̅ - M) / S always lies between -3 and +3.

(iii) The mode is said to be ill-defined in the following situation:

(a) if the frequency distribution has classes of unequal length.

(b) if the frequency distribution is a mixed type (partly discrete and partly continuous).

(c) If the frequency distribution has been more than one mode. In this situation, the following formulae are used.

sk =  3 (X̅ - M) and j = 3 (X̅ - M) / S 

(2) Bowley’s Method :

Base: In a skewed frequency distribution, both the quartile Q₁ and Q₃ are not equi-distant from the median. i.e. Q₃ – M not equal to  M – Q₁. Bowley’s method is based on this test of skewness. 

Formulae: The difference between the distance Q₃ – M and M – Q₁ is taken as the absolute measure of skewness (sk). 

i.e. Skewness (sk) =    (Q₃ – M) – (M – Q₁)

 =     Q₃ – M – M + Q₁

 Skewness (sk) = Q₃ + Q₁ – 2M 

The coefficient of skewness is obtained by dividing the above difference by the sum of the distance Q₃ – M and M – Q_1. 

coefficient of skewness (j) = Q₃ + Q₁ – 2M / Q₃ - Q₁ 

Note: the value of the coefficient of skewness (j) given by Bowley’s method always lies between -1 and +1. 

Comparison of Karl Pearson's Method and Bowley's Method.

1. As Karl Pearson's method and Bowley's method are based on different assumptions, the values of the coefficient of skewness obtained by the two methods may not be equal.

 

2.  The calculations are simple and easy in Bowley's method, whereas the calculations are not simple in taking more time in Karl Pearson's method.

3. The co-efficient of skewness obtained by Karl Pearson's method is more reliable than Bowley's method. Karl Pearson's formula off is based on mean X and standard deviation (S) which are the best measures of average and dispersion. 

4. Karl Pearson's method cannot be used for open-end frequency distribution. When open-end frequency distribution is given then Bowley's method is to be used. 

Points to be remembered while solving examples

(1) If it is not stated by which method co-efficient of skewness is to be calculated in the example, then use Karl Pearson's method. 

(2) If the frequency distribution is open-end frequency distribution, then use Bowley's method for calculating the coefficient of skewness. 

(3) In a given frequency distribution, the observations or the classes are to be arranged in ascending order if they are not in ascending order.  

(4) If the classes of a given frequency distribution are exclusive, then find boundary points for the corresponding classes for calculating median, mode, or quartiles. 

(5) If the cumulative frequency distribution of 'less than type' or 'more than type' is given, then convert it into an original frequency distribution. 

(6) If instead of classes, the mid-values are given then first find boundary points for

 each mid-value by the following formulae.

  Lower boundary point = Mid-value -  (Class interval / 2)

 Upper boundary point = Mid-value +  (Class interval / 2)

(7) If mode is ill-defined, then for Karl Pearson's method use the following formulae.  

sk =  3 (X̅ - M) and j = 3 (X̅ - M) / S 

(8) If a given frequency distribution is of unequal class interval or of mixed type i.e. partly discrete and partly continuous, then for calculation of mean and standard1 deviation by short cut method class interval (C) should not be taken.

(9) The value of the coefficient of skewness may be positive, negative, or zero.

Kurtosis

Kurtosis refers to the degree of presence of outliers in the distribution.

Kurtosis is a statistical measure, whether the data is heavy-tailed or light-tailed in a normal distribution.

In finance, kurtosis is used as a measure of financial risk. A large kurtosis is associated with a high level of risk for an investment because it indicates that there are high probabilities of extremely large and extremely small returns. 

On the other hand, a small kurtosis signals a moderate level of risk because the probabilities of extreme returns are relatively low.

Excess Kurtosis

The excess kurtosis is used in statistics and probability theory to compare the kurtosis coefficient with that normal distribution. 

Excess kurtosis can be positive (Leptokurtic distribution), negative (Platykurtic distribution), or near to zero (Mesokurtic distribution). Since normal distributions have a kurtosis of 3, excess kurtosis is calculating by subtracting kurtosis by 3.

               Excess kurtosis  =  Kurt – 3

Types of excess kurtosis

1. Leptokurtic or heavy-tailed distribution (kurtosis more than normal distribution).
2. Mesokurtic (kurtosis same as the normal distribution).
3. Platykurtic or short-tailed distribution (kurtosis less than normal distribution).

Leptokurtic (kurtosis > 3)

Leptokurtic is having very long and skinny tails, which means there are more chances of outliers. Positive values of kurtosis indicate that distribution is peaked and possesses thick tails. 

An extreme positive kurtosis indicates a distribution where more of the numbers are located in the tails of the distribution instead of around the mean.

platykurtic (kurtosis < 3)

Platykurtic having a lower tail and stretched around center tails means most of the data points are present in high proximity with mean. 

A platykurtic distribution is flatter (less peaked) when compared with the normal distribution.

Mesokurtic (kurtosis = 3)

Mesokurtic is the same as the normal distribution, which means kurtosis is near to 0. 

In Mesokurtic, distributions are moderate in breadth, and curves are a medium peaked height.

Summary

The skewness is a measure of symmetry or asymmetry of data distribution, and kurtosis measures whether data is heavy-tailed or light-tailed in a normal distribution. 

Data can be positive-skewed (data-pushed towards the right side) or negative-skewed (data-pushed towards the left side).

When data skewed, the tail region may behave as an outlier for the statistical model, and outliers unsympathetically affect the model’s performance especially regression-based models. 

Some statistical models are hardy to outliers like Tree-based models, but it will limit the possibility to try other models. So there is a necessity to transform the skewed data to close enough to a Normal distribution.

Excess kurtosis can be positive (Leptokurtic distribution), negative (Platykurtic distribution), or near to zero (Mesokurtic distribution).

Leptokurtic distribution (kurtosis more than normal distribution). Mesokurtic distribution (kurtosis same as the normal distribution). Platykurtic distribution (kurtosis less than normal distribution).